Triángulo de Pascal y Su Relación Con El Binomio de Newton

Historia

Blaise Pascal

Triángulo de Pascal también conocido como Triángulo de Tartaglia es una representación de los coeficientes binomiales, esta clasificación se encuentra acomodada en forma a un triángulo.

La notación fue incluida en la obra de Blaise Pascal "Traité du triangle arithmétique" durante 1654, quiénes descubrieron esta aportación fueron antiguos chinos e indios, mas fue el matemático Pascal quién lo desarrollo y perfeccionó.

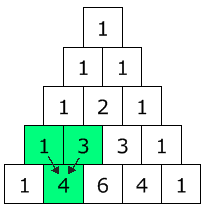
Triángulo de Pascal

La forma comienza con el número "1" en punta ,  debajo de el se encuentran una serie de números de tal manera que cada número es el resultado de la suma de sus 2 números superiores, a excepción de los extremos que siempre son 1.

Como se puede observar la suma de 1+3= 4, lo cual cumple con lo ya mencionado, "cada número es el resultado de la suma de sus 2 números superiores"

Propiedades del Triángulo                            

• Diagonales

1º Diagonal : Solo "1".                                           

2º Diagonal: Números Consecutivos

3º Diagonal: Números Triangulares

• Suma Horizontal

La suma de los números horizontales ( filas).

Como se puede observar el resultado de las sumas   

es el doble de la anterior.                                              

Binomio de Newton

La fórmula que nos permite hallar las potencias de un binomio se conoce como "Binomio de Newton". Con esta se deduce la fórmula que permite elevar a cualquier potencia de exponente natural," n" , un binomio. 

La forma empleada es: (a+b)ⁿ

Esta se puede ocupar para elevar a cualquier potencia, y se desarrolla de la siguiente manera. Ejemplo: 

Se puede observar que el número de término se puede obtener por: n+1.

Importante: en caso de que uno de los términos del binomio sea negativo (-), se deberán de alternar los signos positivos y negativos.

Relación con el Triángulo de Pascal

Los coeficientes de los binomios son números combinatorios los cuales se pueden obtener a partir del Triángulo de Pascal.

Si se observan los coeficientes de cada polinomio de los ejemplos anteriores, podemos observar una secuencia: 

Este es el Triángulo de Pascal
( filas de los números combinatorios)

Es decir cada que cada uno de esos números corresponden al valor de un número combinatorio :

Cada fila empieza y termina por el "1".
(Forman una fila simétrica)

Tip:

Una forma de evitar tener que calcular uno a uno todos los coeficientes ( ósea la fórmula) ,  es utilizar el Triángulo de Pascal, ya que los coeficientes de la potencia n aparecen en la fila n+1 de dicho triángulo

Resumen:

"La fórmula general del llamado Binomio de Newton (a + b)ⁿ está formada por unos coeficientes que coinciden con la línea número n+1 del triángulo de Pascal (la que empieza por 1 y n)."

Operaciones con Polinomios.

Los polinomios son expresiones algebraicas las cuales
están compuestas por 3 o mas términos.

- Nota-

El exponente de todo término en un polinomio
debe ser un número Natural, es decir, a partir del 1…2…3…

Suma

Para realizar la operación se deben de sumar los coeficientes de los términos del mismo grado, a continuación paso a paso el como hacerlo:

1. Se ordenan los polinomios ( en caso de que no lo estén). 

2. Como siguiente, se agrupan los términos del mismo grado.

3. Se suman los términos semejantes. Ejemplo:

                                                          

         

Resta

La resta de polinomios consiste en sumar al minuendo el  opuesto del substraendo. Igual que en la suma de enteros, se cambia a suma del opuesto o inverso aditivo.

1. Se ordenan los términos dependiendo su grado.

2. Un polinomio se cambia a suma del opuesto ( inverso aditivo ( signo contrario))

3. Adjuntan los términos del mismo grado.

4. Se realizan las operaciones.

    

Ejemplo :





Multiplicación:

1. Se multiplica cada monomio del primero polinomio por cada término del 2º polinomio.
2.  Se colocan los resultados de la multiplicación.
3. Se ordenan los términos según su grado.
4. Se suman.

Ejemplo:








División

 Para entender con mayor precisión la división de polinomios, nos basaremos de un ejercicio para su explicación detallada.Para dividir dos polinomios se procede de la manera siguiente:

1)      Se ordena el dividendo y el divisor  con respecto a una misma letra.

2)      Se divide el primer término del dividendo entre el primer término del divisor, obteniéndose así el primer término del cociente

3)      Se multiplica el primer término del cociente por todo el divisor y el producto así obtenido se resta del dividendo, para lo cual se le cambia de signo y se escribe cada término de su semejante. En el caso de que algún término de este producto no tenga ningún término semejante en el dividendo, es escribe dicho término en el lugar que le corresponda de acuerdo con la ordenación del dividendo y del divisor.

4)      Se divide el primer término del resto entre el primer término del divisor, obteniéndose de este modo el segundo término del cociente.

5)      El segundo término del cociente  se multiplica por todo el divisor y el producto así obtenido se resta del dividendo, cambiándole todos los signos.

6)      Se divide el primer término del segundo resto entre el primer término del divisor y se 

repiten las operaciones anteriores hasta obtener cero como resto.

Papiro de Moscú

En el problema 14º del papiro de Moscú (ca. 1890 a. C.) 

se pide calcular el volumen de un tronco de pirámide

cuadrangular; con esto busco una solución basándose y

recreando polinomios. 

Por lo que se deduce que aquí fue donde nació las 

expresiones algebraicas conocidas como " Polinomios".